01 POTENCIAÇÃO, RADICIAÇÃO E EXPRESSÕES NUMÉRICAS
- Jailson Rodrigues

- 16 de abr. de 2025
- 6 min de leitura

POTENCIAÇÃO
A potenciação é uma operação matemática que representa a multiplicação repetida de um número por si mesmo. Ela é composta por dois elementos principais:

Base (a): O número que será multiplicado por si mesmo.
Expoente (n): Indica quantas vezes a base será multiplicada.
A expressão geral é escrita como aⁿ, que significa a × a × a × ... × a (n vezes).
Uma potência pode ser lida de diferentes formas, dependendo do expoente:
2³ pode ser lido como:
"2 elevado ao cubo" (quando o expoente é 3).
"2 elevado à terceira potência".
"2 elevado a 3".
Exemplos de Cálculo
2³ = 2 × 2 × 2 = 8
5⁴ = 5 × 5 × 5 × 5 = 625
Casos Especiais da Potenciação
1. Expoente Zero (a⁰ = 1)
Qualquer número (exceto zero) elevado a zero é igual a 1:
1⁰ = 1
1.000.000⁰ = 1
(–5)⁰ = 1
2. Expoente Um (a¹ = a)
Todo número elevado a 1 é igual a ele mesmo:
2¹ = 2
200¹ = 200
3. Expoente Negativo (a⁻ⁿ = 1/aⁿ)
Um expoente negativo indica o inverso da base elevada ao expoente positivo:
2⁻¹ = ½
5⁻² = 1/5² = 1/25
350⁻¹ = 1/350
----------------------------------------------------------------------
O que é o inverso de um número?
Todo número pode ser visto como uma fração com denominador 1:
2 = 2/1
5 = 5/1
O inverso de um número é obtido trocando numerador e denominador:
Inverso de 2 → ½
Inverso de 3/4 → 4/3
---------------------------------------------------------------------
Potência de Potência
Quando uma potência está elevada a outro expoente, existem duas formas de resolver, dependendo dos parênteses:
1. Sem Parênteses (aⁿᵐ): Resolve-se de cima para baixo (potência da potência)
3^2^2 = 3⁴ = 81 (pois 2² = 4, e 3⁴ = 81)
23^3^2 = 2⁹ = 512 (3² = 9, e 2⁹ = 512)
2. Com Parênteses ((aⁿ)ᵐ): Multiplicam-se os expoentes
(3²)² = 3⁴ = 81 (2 × 2 = 4)
(5²)³ = 5⁶ = 15.625 (2 × 3 = 6)
--------------------------------------------------------------------------
Observação: Os resultados coincidem quando os expoentes são iguais, mas diferem em outros casos.
--------------------------------------------------------------------------
Base Negativa
O sinal do resultado depende se a base está entre parênteses e do expoente:
1. Sem Parênteses (–aⁿ): O sinal negativo é mantido
–2² = –(25²) = –625 (não confundir com (–25)²)
–4³ = –(4³) = –64
2. Com Parênteses (–a)ⁿ: O sinal depende do expoente
Expoente par → Resultado positivo
(–3)² = 9
(–5)⁴ = 625
Expoente ímpar → Resultado negativo
(–2)³ = –8
(–4)⁵ = –1024
Operações com Potências
Em expressões matemáticas, resolvem-se primeiro as potências, seguindo a ordem das operações.
1. Soma e Subtração
Calculam-se as potências primeiro e depois somam-se ou subtraem-se os resultados:
5² + 4² = 25 + 16 = 41
3³ – 2³ = 27 – 8 = 19
2. Multiplicação
a) Bases iguais: Repete-se a base e somam-se os expoentes
3⁵ × 3³ = 3⁸ = 6.561
b) Bases diferentes: Calculam-se as potências e multiplicam-se os resultados
2² × 4² = 4 × 16 = 64
3. Divisão
a) Bases iguais: Repete-se a base e subtraem-se os expoentes
3⁵ ÷ 3³ = 3² = 9
b) Bases diferentes: Calculam-se as potências e dividem-se os resultados
4² ÷ 3² = 16 ÷ 9 ≈ 1,777...
RADICIAÇÃO
A radiciação é a operação inversa da potenciação. Enquanto na potenciação buscamos o resultado de um número multiplicado por si mesmo n vezes, na radiciação partimos do resultado (radicando) e do número de repetições (índice) para descobrir a base original.
Estrutura da Radiciação
Um radical (√) é representado por:

Índice (n): Indica quantas vezes a base foi multiplicada para obter o radicando.
Radicando: O número dentro do radical, resultado da potenciação.
Raiz: O valor que, elevado ao índice, reproduz o radicando
Exemplo Básico
Sabemos que 3²=9, então:
√9=3(pois 3 × 3 = 9)
Pergunta: Qual número multiplicado por ele mesmo duas vezes resulta em 9?Resposta: 3.
Casos Especiais da Radiciação
1. Raiz de 1
Qualquer raiz de 1 é igual a 1, pois 1ⁿ = 1:

2. Radicando Negativo
O resultado depende do índice:
a) Índice Ímpar
A raiz é real e negativa (assim como na potenciação com base negativa):

b) Índice Par
Não existe raiz real (pois nenhum número real elevado a um expoente par resulta em um valor negativo):
√-16 não tem solução real.
Relação entre Radiciação e Potenciação Fracionária
Uma raiz pode ser convertida em uma potência com expoente fracionário:

--------------------------------------------------------------------------
Regra mnemônica:"Quem está no sol (índice) vai para a sombra (denominador), e quem está na sombra (expoente do radicando) vai para o sol (numerador)."
--------------------------------------------------------------------------
Exemplo:

Radical de Radical (Raiz de Raiz)
Quando um radical está dentro de outro, multiplicamos os índices:

Exemplo:

Operações com Radicais
1. Adição e Subtração
a) Radicandos e Índices Diferentes
Resolve-se cada raiz separadamente e depois soma/subtrai:
√4 + √25 = 2 + 5 = 7
b) Radicandos e Índices Iguais
Soma-se/subtrai-se os coeficientes e mantém-se o radical:
√6 + √6 = 2√6
5√3 - 2√3 = 3√3
2. Multiplicação
a) Índices Iguais
Multiplicam-se os radicandos e simplifica-se:
√4×√4= √16 = 4
√25×√4 = √100 = 10
b) Índices Diferentes
Reduz-se ao mesmo índice (usando MMC) ou resolve-se separadamente:

3. Divisão
a) Índices Iguais
Divide-se os radicandos e simplifica-se:
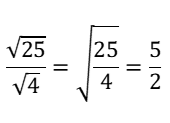
b) Índices Diferentes
Reduz-se ao mesmo índice ou resolve-se separadamente:

Simplificação de Radicais
Quando o radicando é grande, podemos fatorá-lo em potências que facilitem a extração da raiz.
Método de Fatoração
Decomponha o radicando em fatores primos ou produtos conhecidos.
Separe potências que sejam múltiplas do índice.
Extraia do radical os fatores cujos expoentes coincidam com o índice.
Exemplos:
1. Simplificando √900


2. Simplificando √750


3. Simplificando ^3√500


--------------------------------------------------------------------------
Observação: Se não for possível extrair uma raiz exata, o radical permanece simplificado na forma mais reduzida possível.
--------------------------------------------------------------------------
EXPRESSÕES NUMÉRICAS
As expressões numéricas são combinações de números e operações matemáticas que devem ser resolvidas seguindo uma ordem hierárquica definida por regras universais. Essa ordem é essencial para garantir que todos cheguem ao mesmo resultado ao resolver uma mesma expressão.
Hierarquia das Operações
A ordem correta para resolver expressões numéricas é determinada por dois critérios principais:
1. Prioridade dos Símbolos de Agrupamento
Os símbolos definem quais operações devem ser resolvidas primeiro:
Parênteses ( ) → Mais interno
Colchetes [ ] → Intermediário
Chaves { } → Mais externo
2. Ordem das Operações Matemáticas
Dentro de cada agrupamento, as operações devem ser executadas na seguinte sequência:
Potenciação e Radiciação (resolva da esquerda para a direita)
Multiplicação e Divisão (resolva da esquerda para a direita)
Adição e Subtração (resolva da esquerda para a direita)
--------------------------------------------------------------------------
Regra mnemônica: "Parece Realmente Muito Difícil Somar Subtrações?"
(Potências e Raízes → Multiplicações e Divisões → Somas e Subtrações)
--------------------------------------------------------------------------
Exemplos Resolvidos
Exemplo 1: Operações Básicas
(2+5×2)+10
Passo a Passo:
Parênteses:
Dentro dos parênteses, primeiro resolvemos a multiplicação:
5×2=10
Depois a soma:
2+10=12
Fora dos parênteses:
Agora, somamos o resultado com 10:
12+10=22
Resposta Final:
22
Exemplo 2: Expressão com múltiplos agrupamentos
{[5²−10]+(2+3×2)}{[52−10]+(2+3×2)}
Passo a Passo:
Potenciação dentro dos colchetes:
5²=25
Subtração dentro dos colchetes:
25−10=15
Parênteses:
Primeiro, multiplicação:
3×2=6
Depois, soma:
2+6=8
Soma dentro das chaves:
15+8=23
Resposta Final:
23
Exemplo 3: Expressão com divisão e potenciação
{10²×2−100}+[2+(50/2)]+9/3−5
Passo a Passo:
Potenciação dentro das chaves:
10²=100
Multiplicação dentro das chaves:
100×2=200
Subtração dentro das chaves:
200−100=100
Divisão dentro dos colchetes:
50/2=25
Soma dentro dos colchetes:
2+25=27
Divisão fora dos agrupamentos:
9/3=3
Somas e subtrações finais (da esquerda para a direita):
100+27+3−5=125
Resposta Final:
125
Exemplo 3: Expressão com potenciação e radiciação
Expressão original:
2500 - {[5³ + 15] + 7×√6400} + (45 - 2×3²)
Resolver as potências e raízes
5³ = 125
3² = 9
√6400 = 80 (pois 80×80=6400)
Substituindo:
2500 - {[125 + 15] + 7×80} + (45 - 2×9)
Resolver as operações dentro dos parênteses e colchetes
[125 + 15] = 140
7×80 = 560
2×9 = 18
(45 - 18) = 27
Agora a expressão fica:
2500 - {140 + 560} + 27
Resolver as chaves
{140 + 560} = 700
Agora temos:
2500 - 700 + 27
Resolver as operações restantes (da esquerda para direita)
2500 - 700 = 1800
1800 + 27 = 1827
Resposta final: 1827
VAMOS PRATICAR!?
Os links indicados foram acessados em 15 de abril de 2025.



Comentários