TERMINOLOGIAS MATEMÁTICAS NA ECONOMIA: UMA DISCUSSÃO BREVE COM ÊNFASE EM CONCEITOS ECONÔMICOS
- Jailson Rodrigues

- 27 de mai. de 2024
- 6 min de leitura
Atualizado: 13 de fev. de 2025

A Ciência Econômica moderna integra formalizações matemáticas, lógica e estratégias de demonstração em grande parte de seus fundamentos, tornando-se ainda mais evidente nos cursos de pós-graduação que seguem o mainstream. Embora a economia seja uma ciência social aplicada e não uma ciência exata madura, ela faz um uso intensivo da matemática.
O formalismo matemático e estatístico permite que a economia não se concentre apenas na intuição econômica e seus aspectos puramente abstratos, mas também considere sua dimensão aplicada. Outro aspecto importante da Ciência Econômica atual é seu caráter fortemente empírico (e data-driven), com modelos que podem ser estimados a partir da Econometria.
Durante os últimos 30 anos, a Matemática emergiu como a “linguagem da economia”. Hoje em dia, os economistas vêem a Matemática como uma ferramenta inestimável em todos os níveis de estudo, abrangendo desde a expressão da estatística de tendencias do mundo real até o desenvolvimento de sistemas econômicos complemente abstratos (SIMON; BLUME, 2006, p.27).
Grande parte dos problemas econômicos envolve a noção de agentes otimizadores, o que permite tratá-los como análises de custo-benefício. Portanto, os estudantes de Economia precisam ter um conhecimento razoável de Estatística (descritiva, probabilidade e inferência), Cálculo Diferencial e Integral, Lógica Proposicional e Teoria dos Conjuntos na graduação, além de Álgebra Linear, Análise na Reta e Medida de Integração na pós-graduação. No entanto, isso pode variar de acordo com o programa específico.
O grande desafio reside em conciliar o rigor matemático com a intuição econômica, já que ambos se complementam. O economista não se restringe ao papel de matemático ou sociólogo/filósofo, mas atua como um profissional que transita entre esses domínios. Mais precisamente, ele procura modelar os problemas diversos sob uma estrutura de mercado, considerando demanda, oferta, preço e quantidade, e testando suas hipóteses, quando possível, por meio de técnicas econométricas e métodos experimentais ou quase-experimentais.
[...] a abordagem matemática teria razão de proclamar as seguintes vantagens: (1) a “linguagem” utilizada é mais concisa e precisa; (2) existe uma profusão de teoremas matemáticos a nosso dispor; (3) como nos obriga a enunciar explicitamente todas as nossas premissas como um pré-requisito da utilização dos teoremas matemáticos, ela nos resguarda da armadilha de adotar indevidamente premissas indesejáveis; e (4) nos permite tratar o caso geral de n variáveis (CHIANG; WAINWRIGHT, 2006, p.4).
Na formulação de modelos econômicos, busca-se o rigor das demonstrações matemáticas, incorporando termos como definição, hipótese, axioma, lema, teorema, corolário, entre outros. Este artigo tem como objetivo esclarecer esses conceitos, contextualizando-os na teoria econômica (micro e macro). Embora não se aprofunde na formalidade matemática das provas, destaca onde cada termo se encaixa exatamente.
Definição
A definição consiste em explicar o significado de um termo. Podemos formalmente descrever o conjunto orçamentário competitivo (ou walrasiano) da seguinte maneira:
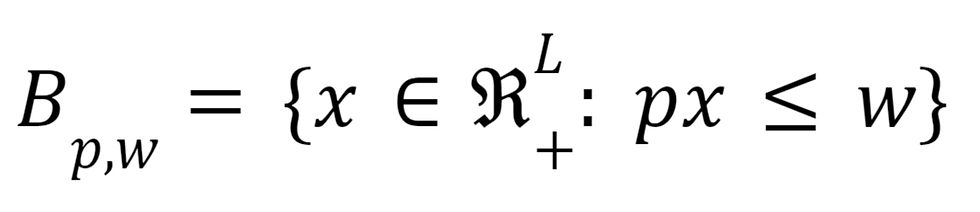
em palavras, dada uma renda (w) e um determinado vetor de preços (p), temos o conjunto de todas as possíveis combinações de consumo de bens (x) que um consumidor pode alcançar dentro de sua restrição orçamentária. Note que estamos apenas definindo o que na teoria microeconômica é conhecido como conjunto orçamentário. Podemos usar essas definições no processo de demonstração.
Hipótese
Refere-se a uma suposição feita sobre uma questão específica. As hipóteses podem ser testadas empiricamente ou utilizadas simplesmente para simplificar o raciocínio, mesmo que sejam irrealistas.
Alguns exemplos:
"Os gastos das pessoas são sempre menores ou iguais as suas rendas";
"Uma economia fechada e sem governo";
"Os indivíduos poupam uma fração constante da renda";
"Mais escolaridade implica em maiores salários";
"Mais armas, menos crimes".
Um exemplo de postulado sobre as preferências do consumido é a convexidade:

Essa hipótese sugere que a média é preferível aos extremos, ou que a diversificação é mais desejável do que a especialização. Em termos simples, quando um consumidor que segue essa hipótese vai ao mercado, ele fica mais satisfeito ao voltar para casa com uma cesta contendo diversos tipos de bens do que se tivesse comprado uma grande quantidade de um único produto.
Ponto importante: uma hipótese que exige demonstração é um teorema, enquanto uma hipótese aceita sem necessidade de prova é um axioma.
Axioma
Um axioma é uma premissa considerada necessariamente evidente e verdadeira. Por ser aceito como verdadeiro sem a necessidade de demonstração (prova), o axioma serve como base fundamental para a construção de teorias. Na microeconomia canônica, as preferências do consumidor são caracterizadas de forma axiomática, ou seja, através da imposição de axiomas que definem propriedades básicas e intuitivas das escolhas do consumidor.
Esses axiomas são essenciais para desenvolver modelos econômicos que possam prever e analisar o comportamento do consumidor de maneira lógica e consistente. Vejamos três axiomas fundamentais da Teoria da Escolha Do Consumidor:
Completude
O axioma da completude estabelece que o consumidor pode sempre comparar qualquer par de cestas de bens. Isso significa que, para quaisquer duas cestas de bens A e B, o consumidor pode decidir se prefere 𝐴 a 𝐵, B a 𝐴 , ou se é indiferente entre ambas.

Reflexividade
O axioma da reflexividade afirma que qualquer cesta de bens é, pelo menos, tão boa quanto ela mesma.

Em outras palavras, o consumidor considera uma cesta A sempre tão boa quanto a própria cesta A.
Transitividade
O axioma da transitividade garante a consistência das preferências do consumidor.
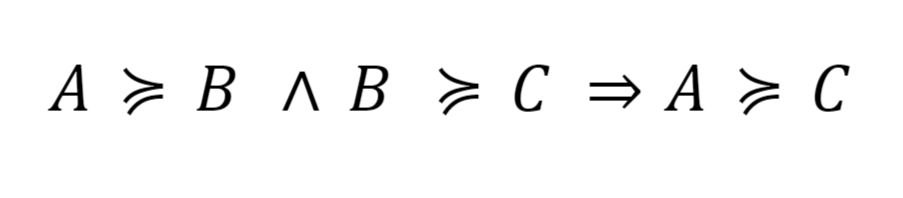
Significa que se o consumidor prefere a cesta A à cesta B e prefere a cesta B à cesta C, então ele também prefere a cesta A à cesta C.
Portanto, esses axiomas são essenciais para garantir que as preferências do consumidor possam ser representadas de maneira consistente e útil em análises econômicas.
Teorema
Um teorema é uma proposição cuja veracidade foi demonstrada (ou provada) formalmente. Na prática, o termo teorema é atribuído a resultados importantes. Explorando um pouco além do escopo da Microeconomia, há um importante teorema na Macroeconomia, denominado Teorema da Equivalência Ricardiana. Este teorema postula que o financiamento da dívida por meio da emissão de títulos apenas adia a tributação e, portanto, em muitos casos, é estritamente equivalente à tributação atual [ver Dornbusch, Fischer e Startz (2013)].
Existe também o Teorema de Euler, oriundo do cálculo multivariado, que possui diversas aplicações na Ciência Econômica, tanto na Microeconomia [ver Nicholson e Snyder (2016) ] quanto na Macroeconomia [ver Mankiw (2015)].
Corolário
Um corolário é um resultado derivado diretamente de um teorema já provado. Como o corolário decorre de um teorema demonstrado verdadeiro, ele também deve ser verdadeiro.
O chamado "efeito de substituição de Arrow" é um resultado relevante que indica que, em uma estrutura de mercado monopolista, há menos estímulos para inovação em comparação com uma empresa em um mercado competitivo. Para o monopolista, inovar significaria "substituir" os lucros que já obtém, reduzindo o incentivo para buscar novas inovações.
Um corolário imediato é que um potencial entrante teria incentivos mais fortes para inovar, dado que a firma competitiva tem lucro normal e não possui lucro existente a ser substituído (ACEMOGLU, 2009, p.421).
Lema
Um lema é um resultado teórico utilizado como um passo intermediário na demonstração de um teorema mais importante subsequente. Sua importância reside na sua utilidade para comprovar outros teoremas.
O "Lema de Shephard", amplamente empregado na microeconomia, é chamado de "lema" porque desempenha um papel crucial na construção de resultados mais abrangentes [ver Nicholson e Snyder (2016)]. Por exemplo, usando esse lema, podemos demonstrar que a função de demanda compensada para um bem pode ser derivada diretamente da função de despesa por meio da diferenciação.
Assim, enquanto o lema é instrumental na comprovação do teorema principal, o corolário é uma implicação imediata desse teorema.
Prova (demonstração)
A prova é a explicação que justifica por que uma proposição é verdadeira. Geralmente, consiste em uma sequência lógica que utiliza os termos e conceitos vistos anteriormente para chegar a um resultado final, validando a proposição.
Um tipo muito comum de demonstração é a prova por absurdo. Esse método consiste em inicialmente supor que algo é verdadeiro e, em seguida, demonstrar como essa suposição leva a uma contradição. Por exemplo, assumimos que A é verdadeiro, o que implica que B não pode ser verdadeiro. Se, ao assumir que A = B, chegamos a uma contradição, concluímos que A não pode ser igual a B.
Atenção! O método por absurdo só funciona quando estamos lidando com situações dicotômicas (se uma coisa for verdadeira, a outra não pode ser).
Outro termo importante é conjectura, que é uma proposição considerada verdadeira, mas para a qual ainda não temos provas. Em demonstrações por absurdo, é comum fazer uso de conjecturas.
Além da prova por contradição, existem outros tipos de demonstração, como a demonstração direta e a demonstração construtiva (por exemplo, a indução).
Referências
ACEMOGLU, Daron. Introduction to Modern Economic Growth. Princeton, NJ: Princeton University Press, 2009.CHIANG, A. C.; WAINWRIGHT, K. Matemática para economistas. – 4. ed. – Rio de Janeiro: Elsevier, 2006.DORNBUSCH, R.; FISCHER, S.; STARTZ, R. Macroeconomia. - 11. ed. - São Paulo: AMGH Editora, 2013.MANKIW, N. G. Macroeconomia. - 8. ed. - Rio de Janeiro: LTC, 2015. NICHOLSON, W.; SNYDER, C. M. Microeconomic Theory: Basic Principles and Extensions. Boston, MA: Cengage Learning, 2016.SIMON, C. P.; BLUME, L. Matemática para economistas. – Porto Alegre: Bookman, 2006.Links adicionais
[3] https://www.youtube.com/watch?v=GTNsRMenKfY [videoaula do canal Matemática Essencial sobre o tema] 



Comentários